Variance
Jump to navigationJump to search
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean. Informally, it measures how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by {\displaystyle \sigma ^{2}}, {\displaystyle s^{2}}, or {\displaystyle \operatorname {Var} (X)}.
Definition[edit]
The variance of a random variable {\displaystyle X} is the expected value of the squared deviation from the mean of {\displaystyle X}, {\displaystyle \mu =\operatorname {E} [X]}:
- {\displaystyle \operatorname {Var} (X)=\operatorname {E} \left[(X-\mu )^{2}\right].}
This definition encompasses random variables that are generated by processes that are discrete, continuous, neither, or mixed. The variance can also be thought of as the covariance of a random variable with itself:
- {\displaystyle \operatorname {Var} (X)=\operatorname {Cov} (X,X).}
The variance is also equivalent to the second cumulant of a probability distribution that generates {\displaystyle X}. The variance is typically designated as {\displaystyle \operatorname {Var} (X)}, {\displaystyle \sigma _{X}^{2}}, or simply {\displaystyle \sigma ^{2}} (pronounced “sigma squared”). The expression for the variance can be expanded as follows:
- {\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}}
In other words, the variance of X is equal to the mean of the square of X minus the square of the mean of X. This equation should not be used for computations using floating point arithmetic, because it suffers from catastrophic cancellation if the two components of the equation are similar in magnitude. For other numerically stable alternatives, see Algorithms for calculating variance.
Discrete random variable[edit]
If the generator of random variable {\displaystyle X} is discrete with probability mass function {\displaystyle x_{1}\mapsto p_{1},x_{2}\mapsto p_{2},\ldots ,x_{n}\mapsto p_{n}}, then
- {\displaystyle \operatorname {Var} (X)=\sum _{i=1}^{n}p_{i}\cdot (x_{i}-\mu )^{2},}
or equivalently,
- {\displaystyle \operatorname {Var} (X)=\left(\sum _{i=1}^{n}p_{i}x_{i}^{2}\right)-\mu ^{2},}
where {\displaystyle \mu } is the expected value. That is,
- {\displaystyle \mu =\sum _{i=1}^{n}p_{i}x_{i}.}
(When such a discrete weighted variance is specified by weights whose sum is not 1, then one divides by the sum of the weights.)
The variance of a collection of {\displaystyle n} equally likely values can be written as
- {\displaystyle \operatorname {Var} (X)={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{2}\right)-\mu ^{2},}
where {\displaystyle \mu } is the average value. That is,
- {\displaystyle \mu ={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.}
The variance of a set of {\displaystyle n} equally likely values can be equivalently expressed, without directly referring to the mean, in terms of squared deviations of all points from each other:[1]
- {\displaystyle \operatorname {Var} (X)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}{\frac {1}{2}}(x_{i}-x_{j})^{2}={\frac {1}{n^{2}}}\sum _{i}\sum _{j>i}(x_{i}-x_{j})^{2}.}
Absolutely continuous random variable[edit]
If the random variable {\displaystyle X} has a probability density function {\displaystyle f(x)}, and {\displaystyle F(x)} is the corresponding cumulative distribution function, then
- {\displaystyle {\begin{aligned}\operatorname {Var} (X)=\sigma ^{2}&=\int _{\mathbb {R} }(x-\mu )^{2}f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}f(x)\,dx-2\mu \int _{\mathbb {R} }xf(x)\,dx+\mu ^{2}\int _{\mathbb {R} }f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \int _{\mathbb {R} }x\,dF(x)+\mu ^{2}\int _{\mathbb {R} }\,dF(x)\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \cdot \mu +\mu ^{2}\cdot 1\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-\mu ^{2},\end{aligned}}}
or equivalently,
- {\displaystyle \operatorname {Var} (X)=\int _{\mathbb {R} }x^{2}f(x)\,dx-\mu ^{2},}
where {\displaystyle \mu } is the expected value of {\displaystyle X} given by
- {\displaystyle \mu =\int _{\mathbb {R} }xf(x)\,dx=\int _{\mathbb {R} }x\,dF(x).}
In these formulas, the integrals with respect to {\displaystyle dx} and {\displaystyle dF(x)} are Lebesgue and Lebesgue–Stieltjes integrals, respectively.
If the function {\displaystyle x^{2}f(x)} is Riemann-integrable on every finite interval {\displaystyle [a,b]\subset \mathbb {R} ,} then
- {\displaystyle \operatorname {Var} (X)=\int _{-\infty }^{+\infty }x^{2}f(x)\,dx-\mu ^{2},}
where the integral is an improper Riemann integral.
Examples[edit]
Exponential distribution[edit]
The exponential distribution with parameter λ is a continuous distribution whose probability density function is given by
- {\displaystyle f(x)=\lambda e^{-\lambda x}}
on the interval [0, ∞). Its mean can be shown to be
- {\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }\lambda xe^{-\lambda x}\,dx={\frac {1}{\lambda }}.}
Using integration by parts and making use of the expected value already calculated, we have:
- {\displaystyle {\begin{aligned}\operatorname {E} \left[X^{2}\right]&=\int _{0}^{\infty }\lambda x^{2}e^{-\lambda x}\,dx\\&=\left[-x^{2}e^{-\lambda x}\right]_{0}^{\infty }+\int _{0}^{\infty }2xe^{-\lambda x}\,dx\\&=0+{\frac {2}{\lambda }}\operatorname {E} [X]\\&={\frac {2}{\lambda ^{2}}}.\end{aligned}}}
Thus, the variance of X is given by
- {\displaystyle \operatorname {Var} (X)=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}={\frac {2}{\lambda ^{2}}}-\left({\frac {1}{\lambda }}\right)^{2}={\frac {1}{\lambda ^{2}}}.}
Fair die[edit]
A fair six-sided die can be modeled as a discrete random variable, X, with outcomes 1 through 6, each with equal probability 1/6. The expected value of X is {\displaystyle (1+2+3+4+5+6)/6=7/2.} Therefore, the variance of X is
- {\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\sum _{i=1}^{6}{\frac {1}{6}}\left(i-{\frac {7}{2}}\right)^{2}\\[5pt]&={\frac {1}{6}}\left((-5/2)^{2}+(-3/2)^{2}+(-1/2)^{2}+(1/2)^{2}+(3/2)^{2}+(5/2)^{2}\right)\\[5pt]&={\frac {35}{12}}\approx 2.92.\end{aligned}}}
The general formula for the variance of the outcome, X, of an n-sided die is
- {\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left(X^{2}\right)-(\operatorname {E} (X))^{2}\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}i^{2}-\left({\frac {1}{n}}\sum _{i=1}^{n}i\right)^{2}\\[5pt]&={\frac {(n+1)(2n+1)}{6}}-\left({\frac {n+1}{2}}\right)^{2}\\[4pt]&={\frac {n^{2}-1}{12}}.\end{aligned}}}
Commonly used probability distributions[edit]
The following table lists the variance for some commonly used probability distributions.
| Name of the probability distribution | Probability distribution function | Mean | Variance |
|---|---|---|---|
| Binomial distribution | {\displaystyle \Pr \,(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}} | {\displaystyle np} | {\displaystyle np(1-p)} |
| Geometric distribution | {\displaystyle \Pr \,(X=k)=(1-p)^{k-1}p} | {\displaystyle {\frac {1}{p}}} | {\displaystyle {\frac {(1-p)}{p^{2}}}} |
| Normal distribution | {\displaystyle f\left(x\mid \mu ,\sigma ^{2}\right)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}} | {\displaystyle \mu } | {\displaystyle \sigma ^{2}} |
| Uniform distribution (continuous) | {\displaystyle f(x\mid a,b)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[3pt]0&{\text{for }}x<a{\text{ or }}x>b\end{cases}}} | {\displaystyle {\frac {a+b}{2}}} | {\displaystyle {\frac {(b-a)^{2}}{12}}} |
| Exponential distribution | {\displaystyle f(x\mid \lambda )=\lambda e^{-\lambda x}} | {\displaystyle {\frac {1}{\lambda }}} | {\displaystyle {\frac {1}{\lambda ^{2}}}} |
| Poisson distribution | {\displaystyle f(x\mid \lambda )={\frac {e^{-\lambda }\lambda ^{x}}{k!}}} | {\displaystyle \lambda } | {\displaystyle \lambda } |
Properties[edit]
Basic properties[edit]
Variance is non-negative because the squares are positive or zero:
- {\displaystyle \operatorname {Var} (X)\geq 0.}
The variance of a constant is zero.
- {\displaystyle \operatorname {Var} (a)=0.}
Conversely, if the variance of a random variable is 0, then it is almost surely a constant. That is, it always has the same value:
- {\displaystyle \operatorname {Var} (X)=0\iff \exists a:P(X=a)=1.}
Variance is invariant with respect to changes in a location parameter. That is, if a constant is added to all values of the variable, the variance is unchanged:
- {\displaystyle \operatorname {Var} (X+a)=\operatorname {Var} (X).}
If all values are scaled by a constant, the variance is scaled by the square of that constant:
- {\displaystyle \operatorname {Var} (aX)=a^{2}\operatorname {Var} (X).}
The variance of a sum of two random variables is given by
- {\displaystyle \operatorname {Var} (aX+bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)+2ab\,\operatorname {Cov} (X,Y),}
- {\displaystyle \operatorname {Var} (aX-bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)-2ab\,\operatorname {Cov} (X,Y),}
where {\displaystyle \operatorname {Cov} (X,Y)} is the covariance.
In general, for the sum of {\displaystyle N} random variables {\displaystyle \{X_{1},\dots ,X_{N}\}}, the variance becomes:
- {\displaystyle \operatorname {Var} \left(\sum _{i=1}^{N}X_{i}\right)=\sum _{i,j=1}^{N}\operatorname {Cov} (X_{i},X_{j})=\sum _{i=1}^{N}\operatorname {Var} (X_{i})+\sum _{i\neq j}\operatorname {Cov} (X_{i},X_{j}).}
These results lead to the variance of a linear combination as:
- {\displaystyle {\begin{aligned}\operatorname {Var} \left(\sum _{i=1}^{N}a_{i}X_{i}\right)&=\sum _{i,j=1}^{N}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})\\&=\sum _{i=1}^{N}a_{i}^{2}\operatorname {Var} (X_{i})+\sum _{i\not =j}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})\\&=\sum _{i=1}^{N}a_{i}^{2}\operatorname {Var} (X_{i})+2\sum _{1\leq i<j\leq N}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j}).\end{aligned}}}
If the random variables {\displaystyle X_{1},\dots ,X_{N}} are such that
- {\displaystyle \operatorname {Cov} (X_{i},X_{j})=0\ ,\ \forall \ (i\neq j),}
then they are said to be uncorrelated. It follows immediately from the expression given earlier that if the random variables {\displaystyle X_{1},\dots ,X_{N}} are uncorrelated, then the variance of their sum is equal to the sum of their variances, or, expressed symbolically:
- {\displaystyle \operatorname {Var} \left(\sum _{i=1}^{N}X_{i}\right)=\sum _{i=1}^{N}\operatorname {Var} (X_{i}).}
Since independent random variables are always uncorrelated (see Covariance § Uncorrelatedness and independence), the equation above holds in particular when the random variables {\displaystyle X_{1},\dots ,X_{n}} are independent. Thus, independence is sufficient but not necessary for the variance of the sum to equal the sum of the variances.
Issues of finiteness[edit]
If a distribution does not have a finite expected value, as is the case for the Cauchy distribution, then the variance cannot be finite either. However, some distributions may not have a finite variance, despite their expected value being finite. An example is a Pareto distribution whose index {\displaystyle k} satisfies {\displaystyle 1<k\leq 2.}
[edit]
One reason for the use of the variance in preference to other measures of dispersion is that the variance of the sum (or the difference) of uncorrelated random variables is the sum of their variances:
- {\displaystyle \operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\sum _{i=1}^{n}\operatorname {Var} (X_{i}).}
This statement is called the Bienaymé formula[2] and was discovered in 1853.[3][4] It is often made with the stronger condition that the variables are independent, but being uncorrelated suffices. So if all the variables have the same variance σ2, then, since division by n is a linear transformation, this formula immediately implies that the variance of their mean is
- {\displaystyle \operatorname {Var} \left({\overline {X}}\right)=\operatorname {Var} \left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\operatorname {Var} \left(X_{i}\right)={\frac {1}{n^{2}}}n\sigma ^{2}={\frac {\sigma ^{2}}{n}}.}
That is, the variance of the mean decreases when n increases. This formula for the variance of the mean is used in the definition of the standard error of the sample mean, which is used in the central limit theorem.
To prove the initial statement, it suffices to show that
- {\displaystyle \operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y).}
The general result then follows by induction. Starting with the definition,
- {\displaystyle {\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[(X+Y)^{2}\right]-(\operatorname {E} [X+Y])^{2}\\[5pt]&=\operatorname {E} \left[X^{2}+2XY+Y^{2}\right]-(\operatorname {E} [X]+\operatorname {E} [Y])^{2}.\end{aligned}}}
Using the linearity of the expectation operator and the assumption of independence (or uncorrelatedness) of X and Y, this further simplifies as follows:
- {\displaystyle {\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[X^{2}\right]+2\operatorname {E} [XY]+\operatorname {E} \left[Y^{2}\right]-\left(\operatorname {E} [X]^{2}+2\operatorname {E} [X]\operatorname {E} [Y]+\operatorname {E} [Y]^{2}\right)\\[5pt]&=\operatorname {E} \left[X^{2}\right]+\operatorname {E} \left[Y^{2}\right]-\operatorname {E} [X]^{2}-\operatorname {E} [Y]^{2}\\[5pt]&=\operatorname {Var} (X)+\operatorname {Var} (Y).\end{aligned}}}
[edit]
With correlation and fixed sample size[edit]
In general, the variance of the sum of n variables is the sum of their covariances:
- {\displaystyle \operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\sum _{i=1}^{n}\sum _{j=1}^{n}\operatorname {Cov} \left(X_{i},X_{j}\right)=\sum _{i=1}^{n}\operatorname {Var} \left(X_{i}\right)+2\sum _{1\leq i<j\leq n}\operatorname {Cov} \left(X_{i},X_{j}\right).}
(Note: The second equality comes from the fact that Cov(Xi,Xi) = Var(Xi).)
Here, Cov(⋅, ⋅) is the covariance, which is zero for independent random variables (if it exists). The formula states that the variance of a sum is equal to the sum of all elements in the covariance matrix of the components. The next expression states equivalently that the variance of the sum is the sum of the diagonal of covariance matrix plus two times the sum of its upper triangular elements (or its lower triangular elements); this emphasizes that the covariance matrix is symmetric. This formula is used in the theory of Cronbach’s alpha in classical test theory.
So if the variables have equal variance σ2 and the average correlation of distinct variables is ρ, then the variance of their mean is
- {\displaystyle \operatorname {Var} \left({\overline {X}}\right)={\frac {\sigma ^{2}}{n}}+{\frac {n-1}{n}}\rho \sigma ^{2}.}
This implies that the variance of the mean increases with the average of the correlations. In other words, additional correlated observations are not as effective as additional independent observations at reducing the uncertainty of the mean. Moreover, if the variables have unit variance, for example if they are standardized, then this simplifies to
- {\displaystyle \operatorname {Var} \left({\overline {X}}\right)={\frac {1}{n}}+{\frac {n-1}{n}}\rho .}
This formula is used in the Spearman–Brown prediction formula of classical test theory. This converges to ρ if n goes to infinity, provided that the average correlation remains constant or converges too. So for the variance of the mean of standardized variables with equal correlations or converging average correlation we have
- {\displaystyle \lim _{n\to \infty }\operatorname {Var} \left({\overline {X}}\right)=\rho .}
Therefore, the variance of the mean of a large number of standardized variables is approximately equal to their average correlation. This makes clear that the sample mean of correlated variables does not generally converge to the population mean, even though the law of large numbers states that the sample mean will converge for independent variables.
I.i.d. with random sample size[edit]
There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size N is a random variable whose variation adds to the variation of X, such that,
- Var(∑X) = E(N)Var(X) + Var(N)E2(X).[5]
If N has a Poisson distribution, then E(N) = Var(N) with estimator N = n. So, the estimator of Var(∑X) becomes nS2X + nX2 giving
- standard error(X) = √[(S2X + X2)/n].
Matrix notation for the variance of a linear combination[edit]
Define {\displaystyle X} as a column vector of {\displaystyle n} random variables {\displaystyle X_{1},\ldots ,X_{n}}, and {\displaystyle c} as a column vector of {\displaystyle n} scalars {\displaystyle c_{1},\ldots ,c_{n}}. Therefore, {\displaystyle c^{\mathsf {T}}X} is a linear combination of these random variables, where {\displaystyle c^{\mathsf {T}}} denotes the transpose of {\displaystyle c}. Also let {\displaystyle \Sigma } be the covariance matrix of {\displaystyle X}. The variance of {\displaystyle c^{\mathsf {T}}X} is then given by:[6]
- {\displaystyle \operatorname {Var} \left(c^{\mathsf {T}}X\right)=c^{\mathsf {T}}\Sigma c.}
This implies that the variance of the mean can be written as (with a column vector of ones)
- {\displaystyle \operatorname {Var} \left({\bar {x}}\right)=\operatorname {Var} \left({\frac {1}{n}}1’X\right)={\frac {1}{n^{2}}}1’\Sigma 1.}
Weighted sum of variables[edit]
The scaling property and the Bienaymé formula, along with the property of the covariance Cov(aX, bY) = ab Cov(X, Y) jointly imply that
- {\displaystyle \operatorname {Var} (aX\pm bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)\pm 2ab\,\operatorname {Cov} (X,Y).}
This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. For example, if X and Y are uncorrelated and the weight of X is two times the weight of Y, then the weight of the variance of X will be four times the weight of the variance of Y.
The expression above can be extended to a weighted sum of multiple variables:
- {\displaystyle \operatorname {Var} \left(\sum _{i}^{n}a_{i}X_{i}\right)=\sum _{i=1}^{n}a_{i}^{2}\operatorname {Var} (X_{i})+2\sum _{1\leq i}\sum _{<j\leq n}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})}
Product of independent variables[edit]
If two variables X and Y are independent, the variance of their product is given by[7]
- {\displaystyle \operatorname {Var} (XY)=[\operatorname {E} (X)]^{2}\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\operatorname {Var} (X)+\operatorname {Var} (X)\operatorname {Var} (Y).}
Equivalently, using the basic properties of expectation, it is given by
- {\displaystyle \operatorname {Var} (XY)=\operatorname {E} \left(X^{2}\right)\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (X)]^{2}[\operatorname {E} (Y)]^{2}.}
Product of statistically dependent variables[edit]
In general, if two variables are statistically dependent, the variance of their product is given by:
- {\displaystyle {\begin{aligned}\operatorname {Var} (XY)={}&\operatorname {E} \left[X^{2}Y^{2}\right]-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\operatorname {E} (X^{2})\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\left(\operatorname {Var} (X)+[\operatorname {E} (X)]^{2}\right)\left(\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\right)\\[5pt]&-[\operatorname {Cov} (X,Y)+\operatorname {E} (X)\operatorname {E} (Y)]^{2}\end{aligned}}}
Decomposition[edit]
The general formula for variance decomposition or the law of total variance is: If {\displaystyle X} and {\displaystyle Y} are two random variables, and the variance of {\displaystyle X} exists, then
- {\displaystyle \operatorname {Var} [X]=\operatorname {E} (\operatorname {Var} [X\mid Y])+\operatorname {Var} (\operatorname {E} [X\mid Y]).}
The conditional expectation {\displaystyle \operatorname {E} (X\mid Y)} of {\displaystyle X} given {\displaystyle Y}, and the conditional variance {\displaystyle \operatorname {Var} (X\mid Y)} may be understood as follows. Given any particular value y of the random variable Y, there is a conditional expectation {\displaystyle \operatorname {E} (X\mid Y=y)} given the event Y = y. This quantity depends on the particular value y; it is a function {\displaystyle g(y)=\operatorname {E} (X\mid Y=y)}. That same function evaluated at the random variable Y is the conditional expectation {\displaystyle \operatorname {E} (X\mid Y)=g(Y).}
In particular, if {\displaystyle Y} is a discrete random variable assuming possible values {\displaystyle y_{1},y_{2},y_{3}\ldots } with corresponding probabilities {\displaystyle p_{1},p_{2},p_{3}\ldots ,}, then in the formula for total variance, the first term on the right-hand side becomes
- {\displaystyle \operatorname {E} (\operatorname {Var} [X\mid Y])=\sum _{i}p_{i}\sigma _{i}^{2},}
where {\displaystyle \sigma _{i}^{2}=\operatorname {Var} [X\mid Y=y_{i}]}. Similarly, the second term on the right-hand side becomes
- {\displaystyle \operatorname {Var} (\operatorname {E} [X\mid Y])=\sum _{i}p_{i}\mu _{i}^{2}-\left(\sum _{i}p_{i}\mu _{i}\right)^{2}=\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2},}
where {\displaystyle \mu _{i}=\operatorname {E} [X\mid Y=y_{i}]} and {\displaystyle \mu =\sum _{i}p_{i}\mu _{i}}. Thus the total variance is given by
- {\displaystyle \operatorname {Var} [X]=\sum _{i}p_{i}\sigma _{i}^{2}+\left(\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2}\right).}
A similar formula is applied in analysis of variance, where the corresponding formula is
- {\displaystyle {\mathit {MS}}_{\text{total}}={\mathit {MS}}_{\text{between}}+{\mathit {MS}}_{\text{within}};}
here {\displaystyle {\mathit {MS}}} refers to the Mean of the Squares. In linear regression analysis the corresponding formula is
- {\displaystyle {\mathit {MS}}_{\text{total}}={\mathit {MS}}_{\text{regression}}+{\mathit {MS}}_{\text{residual}}.}
This can also be derived from the additivity of variances, since the total (observed) score is the sum of the predicted score and the error score, where the latter two are uncorrelated.
Similar decompositions are possible for the sum of squared deviations (sum of squares, {\displaystyle {\mathit {SS}}}):
- {\displaystyle {\mathit {SS}}_{\text{total}}={\mathit {SS}}_{\text{between}}+{\mathit {SS}}_{\text{within}},}
- {\displaystyle {\mathit {SS}}_{\text{total}}={\mathit {SS}}_{\text{regression}}+{\mathit {SS}}_{\text{residual}}.}
Calculation from the CDF[edit]
The population variance for a non-negative random variable can be expressed in terms of the cumulative distribution function F using
- {\displaystyle 2\int _{0}^{\infty }u(1-F(u))\,du-\left(\int _{0}^{\infty }(1-F(u))\,du\right)^{2}.}
This expression can be used to calculate the variance in situations where the CDF, but not the density, can be conveniently expressed.
Characteristic property[edit]
The second moment of a random variable attains the minimum value when taken around the first moment (i.e., mean) of the random variable, i.e. {\displaystyle \mathrm {argmin} _{m}\,\mathrm {E} \left(\left(X-m\right)^{2}\right)=\mathrm {E} (X)}. Conversely, if a continuous function {\displaystyle \varphi } satisfies {\displaystyle \mathrm {argmin} _{m}\,\mathrm {E} (\varphi (X-m))=\mathrm {E} (X)} for all random variables X, then it is necessarily of the form {\displaystyle \varphi (x)=ax^{2}+b}, where a > 0. This also holds in the multidimensional case.[8]
Units of measurement[edit]
Unlike expected absolute deviation, the variance of a variable has units that are the square of the units of the variable itself. For example, a variable measured in meters will have a variance measured in meters squared. For this reason, describing data sets via their standard deviation or root mean square deviation is often preferred over using the variance. In the dice example the standard deviation is √2.9 ≈ 1.7, slightly larger than the expected absolute deviation of 1.5.
The standard deviation and the expected absolute deviation can both be used as an indicator of the “spread” of a distribution. The standard deviation is more amenable to algebraic manipulation than the expected absolute deviation, and, together with variance and its generalization covariance, is used frequently in theoretical statistics; however the expected absolute deviation tends to be more robust as it is less sensitive to outliers arising from measurement anomalies or an unduly heavy-tailed distribution.
Approximating the variance of a function[edit]
The delta method uses second-order Taylor expansions to approximate the variance of a function of one or more random variables: see Taylor expansions for the moments of functions of random variables. For example, the approximate variance of a function of one variable is given by
- {\displaystyle \operatorname {Var} \left[f(X)\right]\approx \left(f'(\operatorname {E} \left[X\right])\right)^{2}\operatorname {Var} \left[X\right]}
provided that f is twice differentiable and that the mean and variance of X are finite.
Population variance and sample variance[edit]
Real-world observations such as the measurements of yesterday’s rain throughout the day typically cannot be complete sets of all possible observations that could be made. As such, the variance calculated from the finite set will in general not match the variance that would have been calculated from the full population of possible observations. This means that one estimates the mean and variance that would have been calculated from an omniscient set of observations by using an estimator equation. The estimator is a function of the sample of n observations drawn without observational bias from the whole population of potential observations. In this example that sample would be the set of actual measurements of yesterday’s rainfall from available rain gauges within the geography of interest.
The simplest estimators for population mean and population variance are simply the mean and variance of the sample, the sample mean and (uncorrected) sample variance – these are consistent estimators (they converge to the correct value as the number of samples increases), but can be improved. Estimating the population variance by taking the sample’s variance is close to optimal in general, but can be improved in two ways. Most simply, the sample variance is computed as an average of squared deviations about the (sample) mean, by dividing by n. However, using values other than n improves the estimator in various ways. Four common values for the denominator are n, n − 1, n + 1, and n − 1.5: n is the simplest (population variance of the sample), n − 1 eliminates bias, n + 1 minimizes mean squared error for the normal distribution, and n − 1.5 mostly eliminates bias in unbiased estimation of standard deviation for the normal distribution.
Firstly, if the omniscient mean is unknown (and is computed as the sample mean), then the sample variance is a biased estimator: it underestimates the variance by a factor of (n − 1) / n; correcting by this factor (dividing by n − 1 instead of n) is called Bessel’s correction. The resulting estimator is unbiased, and is called the (corrected) sample variance or unbiased sample variance. For example, when n = 1 the variance of a single observation about the sample mean (itself) is obviously zero regardless of the population variance. If the mean is determined in some other way than from the same samples used to estimate the variance then this bias does not arise and the variance can safely be estimated as that of the samples about the (independently known) mean.
Secondly, the sample variance does not generally minimize mean squared error between sample variance and population variance. Correcting for bias often makes this worse: one can always choose a scale factor that performs better than the corrected sample variance, though the optimal scale factor depends on the excess kurtosis of the population (see mean squared error: variance), and introduces bias. This always consists of scaling down the unbiased estimator (dividing by a number larger than n − 1), and is a simple example of a shrinkage estimator: one “shrinks” the unbiased estimator towards zero. For the normal distribution, dividing by n + 1 (instead of n − 1 or n) minimizes mean squared error. The resulting estimator is biased, however, and is known as the biased sample variation.
Population variance[edit]
In general, the population variance of a finite population of size N with values xi is given by
-
{\displaystyle {\begin{aligned}\sigma ^{2}&={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}-\mu \right)^{2}={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}^{2}-2\mu x_{i}+\mu ^{2}\right)\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-2\mu \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)+\mu ^{2}\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\mu ^{2}\end{aligned}}}
where the population mean is
- {\displaystyle \mu ={\frac {1}{N}}\sum _{i=1}^{N}x_{i}.}
The population variance can also be computed using
- {\displaystyle \sigma ^{2}={\frac {1}{N^{2}}}\sum _{i<j}\left(x_{i}-x_{j}\right)^{2}={\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}-x_{j}\right)^{2}.}
This is true because
-
{\displaystyle {\begin{aligned}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}-x_{j}\right)^{2}\\[5pt]={}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}^{2}-2x_{i}x_{j}+x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2N}}\sum _{j=1}^{N}\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}\right)+{\frac {1}{2N}}\sum _{i=1}^{N}\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)-\mu ^{2}+{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)\\[5pt]={}&\sigma ^{2}\end{aligned}}}
The population variance matches the variance of the generating probability distribution. In this sense, the concept of population can be extended to continuous random variables with infinite populations.
Sample variance[edit]
In many practical situations, the true variance of a population is not known a priori and must be computed somehow. When dealing with extremely large populations, it is not possible to count every object in the population, so the computation must be performed on a sample of the population.[9] Sample variance can also be applied to the estimation of the variance of a continuous distribution from a sample of that distribution.
We take a sample with replacement of n values Y1, …, Yn from the population, where n < N, and estimate the variance on the basis of this sample.[10] Directly taking the variance of the sample data gives the average of the squared deviations:
- {\displaystyle \sigma _{Y}^{2}={\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}=\left({\frac {1}{n}}\sum _{i=1}^{n}Y_{i}^{2}\right)-{\overline {Y}}^{2}={\frac {1}{n^{2}}}\sum _{i,j\,:\,i<j}\left(Y_{i}-Y_{j}\right)^{2}.}
Here, {\displaystyle {\overline {Y}}} denotes the sample mean:
- {\displaystyle {\overline {Y}}={\frac {1}{n}}\sum _{i=1}^{n}Y_{i}.}
Since the Yi are selected randomly, both {\displaystyle {\overline {Y}}} and {\displaystyle \sigma _{Y}^{2}} are random variables. Their expected values can be evaluated by averaging over the ensemble of all possible samples {Yi} of size n from the population. For {\displaystyle \sigma _{Y}^{2}} this gives:
- {\displaystyle {\begin{aligned}\operatorname {E} [\sigma _{Y}^{2}]&=\operatorname {E} \left[{\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\frac {1}{n}}\sum _{j=1}^{n}Y_{j}\right)^{2}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\operatorname {E} \left[Y_{i}^{2}-{\frac {2}{n}}Y_{i}\sum _{j=1}^{n}Y_{j}+{\frac {1}{n^{2}}}\sum _{j=1}^{n}Y_{j}\sum _{k=1}^{n}Y_{k}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left[{\frac {n-2}{n}}\operatorname {E} \left[Y_{i}^{2}\right]-{\frac {2}{n}}\sum _{j\neq i}\operatorname {E} \left[Y_{i}Y_{j}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\sum _{k\neq j}^{n}\operatorname {E} \left[Y_{j}Y_{k}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\operatorname {E} \left[Y_{j}^{2}\right]\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left[{\frac {n-2}{n}}\left(\sigma ^{2}+\mu ^{2}\right)-{\frac {2}{n}}(n-1)\mu ^{2}+{\frac {1}{n^{2}}}n(n-1)\mu ^{2}+{\frac {1}{n}}\left(\sigma ^{2}+\mu ^{2}\right)\right]\\[5pt]&={\frac {n-1}{n}}\sigma ^{2}.\end{aligned}}}
Hence {\displaystyle \sigma _{Y}^{2}} gives an estimate of the population variance that is biased by a factor of {\displaystyle {\frac {n-1}{n}}}. For this reason, {\displaystyle \sigma _{Y}^{2}} is referred to as the biased sample variance. Correcting for this bias yields the unbiased sample variance, denoted {\displaystyle s^{2}}:
- {\displaystyle s^{2}={\frac {n}{n-1}}\sigma _{Y}^{2}={\frac {n}{n-1}}\left({\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}\right)={\frac {1}{n-1}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}}
Either estimator may be simply referred to as the sample variance when the version can be determined by context. The same proof is also applicable for samples taken from a continuous probability distribution.
The use of the term n − 1 is called Bessel’s correction, and it is also used in sample covariance and the sample standard deviation (the square root of variance). The square root is a concave function and thus introduces negative bias (by Jensen’s inequality), which depends on the distribution, and thus the corrected sample standard deviation (using Bessel’s correction) is biased. The unbiased estimation of standard deviation is a technically involved problem, though for the normal distribution using the term n − 1.5 yields an almost unbiased estimator.
The unbiased sample variance is a U-statistic for the function ƒ(y1, y2) = (y1 − y2)2/2, meaning that it is obtained by averaging a 2-sample statistic over 2-element subsets of the population.
Distribution of the sample variance[edit]
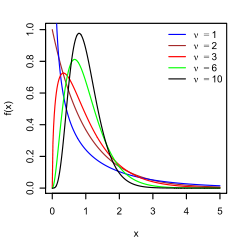
Being a function of random variables, the sample variance is itself a random variable, and it is natural to study its distribution. In the case that Yi are independent observations from a normal distribution, Cochran’s theorem shows that s2 follows a scaled chi-squared distribution:[11]
- {\displaystyle (n-1){\frac {s^{2}}{\sigma ^{2}}}\sim \chi _{n-1}^{2}.}
As a direct consequence, it follows that
- {\displaystyle \operatorname {E} \left(s^{2}\right)=\operatorname {E} \left({\frac {\sigma ^{2}}{n-1}}\chi _{n-1}^{2}\right)=\sigma ^{2},}
and[12]
- {\displaystyle \operatorname {Var} \left[s^{2}\right]=\operatorname {Var} \left({\frac {\sigma ^{2}}{n-1}}\chi _{n-1}^{2}\right)={\frac {\sigma ^{4}}{(n-1)^{2}}}\operatorname {Var} \left(\chi _{n-1}^{2}\right)={\frac {2\sigma ^{4}}{n-1}}.}
If the Yi are independent and identically distributed, but not necessarily normally distributed, then[13]
- {\displaystyle \operatorname {E} \left[s^{2}\right]=\sigma ^{2},\quad \operatorname {Var} \left[s^{2}\right]={\frac {\sigma ^{4}}{n}}\left(\kappa -1+{\frac {2}{n-1}}\right)={\frac {1}{n}}\left(\mu _{4}-{\frac {n-3}{n-1}}\sigma ^{4}\right),}
where κ is the kurtosis of the distribution and μ4 is the fourth central moment.
If the conditions of the law of large numbers hold for the squared observations, s2 is a consistent estimator of σ2. One can see indeed that the variance of the estimator tends asymptotically to zero. An asymptotically equivalent formula was given in Kenney and Keeping (1951:164), Rose and Smith (2002:264), and Weisstein (n.d.).[14][15][16]
Samuelson’s inequality[edit]
Samuelson’s inequality is a result that states bounds on the values that individual observations in a sample can take, given that the sample mean and (biased) variance have been calculated.[17] Values must lie within the limits {\displaystyle {\bar {y}}\pm \sigma _{Y}(n-1)^{1/2}.}
Relations with the harmonic and arithmetic means[edit]
It has been shown[18] that for a sample {yi} of positive real numbers,
- {\displaystyle \sigma _{y}^{2}\leq 2y_{\max }(A-H),}
where ymax is the maximum of the sample, A is the arithmetic mean, H is the harmonic mean of the sample and {\displaystyle \sigma _{y}^{2}} is the (biased) variance of the sample.
This bound has been improved, and it is known that variance is bounded by
- {\displaystyle \sigma _{y}^{2}\leq {\frac {y_{\max }(A-H)(y_{\max }-A)}{y_{\max }-H}},}
- {\displaystyle \sigma _{y}^{2}\geq {\frac {y_{\min }(A-H)(A-y_{\min })}{H-y_{\min }}},}
where ymin is the minimum of the sample.[19]
Tests of equality of variances[edit]
Testing for the equality of two or more variances is difficult. The F test and chi square tests are both adversely affected by non-normality and are not recommended for this purpose.
Several non parametric tests have been proposed: these include the Barton–David–Ansari–Freund–Siegel–Tukey test, the Capon test, Mood test, the Klotz test and the Sukhatme test. The Sukhatme test applies to two variances and requires that both medians be known and equal to zero. The Mood, Klotz, Capon and Barton–David–Ansari–Freund–Siegel–Tukey tests also apply to two variances. They allow the median to be unknown but do require that the two medians are equal.
The Lehmann test is a parametric test of two variances. Of this test there are several variants known. Other tests of the equality of variances include the Box test, the Box–Anderson test and the Moses test.
Resampling methods, which include the bootstrap and the jackknife, may be used to test the equality of variances.
History[edit]
The term variance was first introduced by Ronald Fisher in his 1918 paper The Correlation Between Relatives on the Supposition of Mendelian Inheritance:[20]
The great body of available statistics show us that the deviations of a human measurement from its mean follow very closely the Normal Law of Errors, and, therefore, that the variability may be uniformly measured by the standard deviation corresponding to the square root of the mean square error. When there are two independent causes of variability capable of producing in an otherwise uniform population distributions with standard deviations {\displaystyle \sigma _{1}} and {\displaystyle \sigma _{2}}, it is found that the distribution, when both causes act together, has a standard deviation {\displaystyle {\sqrt {\sigma _{1}^{2}+\sigma _{2}^{2}}}}. It is therefore desirable in analysing the causes of variability to deal with the square of the standard deviation as the measure of variability. We shall term this quantity the Variance…

Geometric visualisation of the variance of an arbitrary distribution (2, 4, 4, 4, 5, 5, 7, 9):
- A frequency distribution is constructed.
- The centroid of the distribution gives its mean.
- A square with sides equal to the difference of each value from the mean is formed for each value.
- Arranging the squares into a rectangle with one side equal to the number of values, n, results in the other side being the distribution’s variance, σ2.
Moment of inertia[edit]
The variance of a probability distribution is analogous to the moment of inertia in classical mechanics of a corresponding mass distribution along a line, with respect to rotation about its center of mass.[citation needed] It is because of this analogy that such things as the variance are called moments of probability distributions.[citation needed] The covariance matrix is related to the moment of inertia tensor for multivariate distributions. The moment of inertia of a cloud of n points with a covariance matrix of {\displaystyle \Sigma } is given by[citation needed]
- {\displaystyle I=n\left(\mathbf {1} _{3\times 3}\operatorname {tr} (\Sigma )-\Sigma \right).}
This difference between moment of inertia in physics and in statistics is clear for points that are gathered along a line. Suppose many points are close to the x axis and distributed along it. The covariance matrix might look like
- {\displaystyle \Sigma ={\begin{bmatrix}10&0&0\\0&0.1&0\\0&0&0.1\end{bmatrix}}.}
That is, there is the most variance in the x direction. Physicists would consider this to have a low moment about the x axis so the moment-of-inertia tensor is
- {\displaystyle I=n{\begin{bmatrix}0.2&0&0\\0&10.1&0\\0&0&10.1\end{bmatrix}}.}
Semivariance[edit]
The semivariance is calculated in the same manner as the variance but only those observations that fall below the mean are included in the calculation:
It is sometimes described as a measure of downside risk in an investments context. For skewed distributions, the semivariance can provide additional information that a variance does not.[21]
For inequalities associated with the semivariance, see Chebyshev’s inequality § Semivariances.
Generalizations[edit]
For complex variables[edit]
If {\displaystyle x} is a scalar complex-valued random variable, with values in {\displaystyle \mathbb {C} ,} then its variance is {\displaystyle \operatorname {E} \left[(x-\mu )(x-\mu )^{*}\right],} where {\displaystyle x^{*}} is the complex conjugate of {\displaystyle x.} This variance is a real scalar.
For vector-valued random variables[edit]
As a matrix[edit]
If {\displaystyle X} is a vector-valued random variable, with values in {\displaystyle \mathbb {R} ^{n},} and thought of as a column vector, then a natural generalization of variance is {\displaystyle \operatorname {E} \left[(X-\mu )(X-\mu )^{\operatorname {T} }\right],} where {\displaystyle \mu =\operatorname {E} (X)} and {\displaystyle X^{\operatorname {T} }} is the transpose of {\displaystyle X,} and so is a row vector. The result is a positive semi-definite square matrix, commonly referred to as the variance-covariance matrix (or simply as the covariance matrix).
If {\displaystyle X} is a vector- and complex-valued random variable, with values in {\displaystyle \mathbb {C} ^{n},} then the covariance matrix is {\displaystyle \operatorname {E} \left[(X-\mu )(X-\mu )^{\dagger }\right],} where {\displaystyle X^{\dagger }} is the conjugate transpose of {\displaystyle X.}[citation needed] This matrix is also positive semi-definite and square.
As a scalar[edit]
Another generalization of variance for vector-valued random variables {\displaystyle X}, which results in a scalar value rather than in a matrix, is the generalized variance {\displaystyle \det(C)}, the determinant of the covariance matrix. The generalized variance can be shown to be related to the multidimensional scatter of points around their mean.[22]
A different generalization is obtained by considering the Euclidean distance between the random variable and its mean. This results in {\displaystyle \operatorname {E} \left[(X-\mu )^{\operatorname {T} }(X-\mu )\right]=\operatorname {tr} (C),} which is the trace of the covariance matrix.
See also[edit]
| Look up variance in Wiktionary, the free dictionary. |
- Bhatia–Davis inequality
- Coefficient of variation
- Homoscedasticity
- Measures for statistical dispersion
- Popoviciu’s inequality on variances





![{\displaystyle \mu =\operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce1b41598b8e8f45f57c1550ebb8d5c7ab8e1210)
![\operatorname {Var} (X)=\operatorname {E} \left[(X-\mu )^{2}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/55622d2a1cf5e46f2926ab389a8e3438edb53731)


![{\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad35c4161b9cf52868e879d457d8d796094ff02)











![{\displaystyle {\begin{aligned}\operatorname {Var} (X)=\sigma ^{2}&=\int _{\mathbb {R} }(x-\mu )^{2}f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}f(x)\,dx-2\mu \int _{\mathbb {R} }xf(x)\,dx+\mu ^{2}\int _{\mathbb {R} }f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \int _{\mathbb {R} }x\,dF(x)+\mu ^{2}\int _{\mathbb {R} }\,dF(x)\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \cdot \mu +\mu ^{2}\cdot 1\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-\mu ^{2},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf3ec706581db5951e939cb3993a5c8289d7da4)





![{\displaystyle [a,b]\subset \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16929783780dae7bb2272902a6ee9345436b481)


![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }\lambda xe^{-\lambda x}\,dx={\frac {1}{\lambda }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc9d5854b87fd1f6a380b1df34d7d9fffcf9b0b)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[X^{2}\right]&=\int _{0}^{\infty }\lambda x^{2}e^{-\lambda x}\,dx\\&=\left[-x^{2}e^{-\lambda x}\right]_{0}^{\infty }+\int _{0}^{\infty }2xe^{-\lambda x}\,dx\\&=0+{\frac {2}{\lambda }}\operatorname {E} [X]\\&={\frac {2}{\lambda ^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/206a5ddf1e6d9ce69e6609c702850172ff3e1311)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}={\frac {2}{\lambda ^{2}}}-\left({\frac {1}{\lambda }}\right)^{2}={\frac {1}{\lambda ^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5064d28d7da067a7a675ae68d992b83bc339c32)

![{\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\sum _{i=1}^{6}{\frac {1}{6}}\left(i-{\frac {7}{2}}\right)^{2}\\[5pt]&={\frac {1}{6}}\left((-5/2)^{2}+(-3/2)^{2}+(-1/2)^{2}+(1/2)^{2}+(3/2)^{2}+(5/2)^{2}\right)\\[5pt]&={\frac {35}{12}}\approx 2.92.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b1b6a74f544d9422366dc015805d67149030ec7)
![{\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left(X^{2}\right)-(\operatorname {E} (X))^{2}\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}i^{2}-\left({\frac {1}{n}}\sum _{i=1}^{n}i\right)^{2}\\[5pt]&={\frac {(n+1)(2n+1)}{6}}-\left({\frac {n+1}{2}}\right)^{2}\\[4pt]&={\frac {n^{2}-1}{12}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a476607e0a4d7f3ba660d8f260abd520b2ffbed)







![{\displaystyle f(x\mid a,b)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[3pt]0&{\text{for }}x<a{\text{ or }}x>b\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49d9ce0f31f14565d14be7083c467987eb0823f)




























![{\displaystyle {\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[(X+Y)^{2}\right]-(\operatorname {E} [X+Y])^{2}\\[5pt]&=\operatorname {E} \left[X^{2}+2XY+Y^{2}\right]-(\operatorname {E} [X]+\operatorname {E} [Y])^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19f68b26d8eddd872d85cb9b846a7b8253c30a18)
![{\displaystyle {\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[X^{2}\right]+2\operatorname {E} [XY]+\operatorname {E} \left[Y^{2}\right]-\left(\operatorname {E} [X]^{2}+2\operatorname {E} [X]\operatorname {E} [Y]+\operatorname {E} [Y]^{2}\right)\\[5pt]&=\operatorname {E} \left[X^{2}\right]+\operatorname {E} \left[Y^{2}\right]-\operatorname {E} [X]^{2}-\operatorname {E} [Y]^{2}\\[5pt]&=\operatorname {Var} (X)+\operatorname {Var} (Y).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a17cef95ad7c7877b877c4e7bb2b3788ff2dde00)














![{\displaystyle \operatorname {Var} (XY)=[\operatorname {E} (X)]^{2}\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\operatorname {Var} (X)+\operatorname {Var} (X)\operatorname {Var} (Y).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/217846baaed2d1a73bd83728419c8199c66c06f0)
![{\displaystyle \operatorname {Var} (XY)=\operatorname {E} \left(X^{2}\right)\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (X)]^{2}[\operatorname {E} (Y)]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60f81d984aa103aed089cc56c27406c845fa50da)
![{\displaystyle {\begin{aligned}\operatorname {Var} (XY)={}&\operatorname {E} \left[X^{2}Y^{2}\right]-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\operatorname {E} (X^{2})\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\left(\operatorname {Var} (X)+[\operatorname {E} (X)]^{2}\right)\left(\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\right)\\[5pt]&-[\operatorname {Cov} (X,Y)+\operatorname {E} (X)\operatorname {E} (Y)]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f71664172a74f8d3dbf6f1b17addf168e55f11)

![{\displaystyle \operatorname {Var} [X]=\operatorname {E} (\operatorname {Var} [X\mid Y])+\operatorname {Var} (\operatorname {E} [X\mid Y]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d096b66af734c89681ab5cb61b24fbea63a48669)







![{\displaystyle \operatorname {E} (\operatorname {Var} [X\mid Y])=\sum _{i}p_{i}\sigma _{i}^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc52b9938aac880c80b76dfe0bacc302c1d0f1d3)
![{\displaystyle \sigma _{i}^{2}=\operatorname {Var} [X\mid Y=y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f02e555171b20f14167f31a43ad480f720a6fa6)
![{\displaystyle \operatorname {Var} (\operatorname {E} [X\mid Y])=\sum _{i}p_{i}\mu _{i}^{2}-\left(\sum _{i}p_{i}\mu _{i}\right)^{2}=\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/069ee9f564216faf173487039b77447b1ef07da2)
![{\displaystyle \mu _{i}=\operatorname {E} [X\mid Y=y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0df777aa646f81fb52b31a3e13f983747fac39dd)

![{\displaystyle \operatorname {Var} [X]=\sum _{i}p_{i}\sigma _{i}^{2}+\left(\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5653ed0b0a55e26b4763766d3e118bc05ed569f4)











![{\displaystyle \operatorname {Var} \left[f(X)\right]\approx \left(f'(\operatorname {E} \left[X\right])\right)^{2}\operatorname {Var} \left[X\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c58412ffa8fdf818b89bafb3318c4ace7cd8e9b)
![{\displaystyle {\begin{aligned}\sigma ^{2}&={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}-\mu \right)^{2}={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}^{2}-2\mu x_{i}+\mu ^{2}\right)\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-2\mu \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)+\mu ^{2}\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\mu ^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e37c1ee507b7c4281e55b812bc3cc4f9b29f490c)


![{\displaystyle {\begin{aligned}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}-x_{j}\right)^{2}\\[5pt]={}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}^{2}-2x_{i}x_{j}+x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2N}}\sum _{j=1}^{N}\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}\right)+{\frac {1}{2N}}\sum _{i=1}^{N}\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)-\mu ^{2}+{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)\\[5pt]={}&\sigma ^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e777ea322a3d824db39d47bcd745c25951bcb33)




![{\displaystyle {\begin{aligned}\operatorname {E} [\sigma _{Y}^{2}]&=\operatorname {E} \left[{\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\frac {1}{n}}\sum _{j=1}^{n}Y_{j}\right)^{2}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\operatorname {E} \left[Y_{i}^{2}-{\frac {2}{n}}Y_{i}\sum _{j=1}^{n}Y_{j}+{\frac {1}{n^{2}}}\sum _{j=1}^{n}Y_{j}\sum _{k=1}^{n}Y_{k}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left[{\frac {n-2}{n}}\operatorname {E} \left[Y_{i}^{2}\right]-{\frac {2}{n}}\sum _{j\neq i}\operatorname {E} \left[Y_{i}Y_{j}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\sum _{k\neq j}^{n}\operatorname {E} \left[Y_{j}Y_{k}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\operatorname {E} \left[Y_{j}^{2}\right]\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left[{\frac {n-2}{n}}\left(\sigma ^{2}+\mu ^{2}\right)-{\frac {2}{n}}(n-1)\mu ^{2}+{\frac {1}{n^{2}}}n(n-1)\mu ^{2}+{\frac {1}{n}}\left(\sigma ^{2}+\mu ^{2}\right)\right]\\[5pt]&={\frac {n-1}{n}}\sigma ^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61d7c57e20c1ae25d4a20478d0dc3e99f1c096d8)





![{\displaystyle \operatorname {Var} \left[s^{2}\right]=\operatorname {Var} \left({\frac {\sigma ^{2}}{n-1}}\chi _{n-1}^{2}\right)={\frac {\sigma ^{4}}{(n-1)^{2}}}\operatorname {Var} \left(\chi _{n-1}^{2}\right)={\frac {2\sigma ^{4}}{n-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab6dfff50a267c642f3b9e51b150761a81bb00ad)
![{\displaystyle \operatorname {E} \left[s^{2}\right]=\sigma ^{2},\quad \operatorname {Var} \left[s^{2}\right]={\frac {\sigma ^{4}}{n}}\left(\kappa -1+{\frac {2}{n-1}}\right)={\frac {1}{n}}\left(\mu _{4}-{\frac {n-3}{n-1}}\sigma ^{4}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e1abcb2ddd063b31acc8ab73edee87d319f3e3c)














![{\displaystyle \operatorname {E} \left[(x-\mu )(x-\mu )^{*}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7cc7933557809745e2928b688000d26478bde22)



![{\displaystyle \operatorname {E} \left[(X-\mu )(X-\mu )^{\operatorname {T} }\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83bab02d13f2da96c2bbc93990454fa364ffea6b)




![{\displaystyle \operatorname {E} \left[(X-\mu )(X-\mu )^{\dagger }\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b430afe926947268de35955a46b5977edadd6a)



![{\displaystyle \operatorname {E} \left[(X-\mu )^{\operatorname {T} }(X-\mu )\right]=\operatorname {tr} (C),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/483e02bc316e8ecfeac1c71f1b2464b4ece2f45c)